TTT Plots

It is a plot of line segments joined between two successive discrete points. These points of scaled TTT and unreliability (CDF) are obtained from the failure data. It gives a picture of failure data in a plot of unit square. If the plot is concave (convex) above (below) the diagonal line, increasing (decreasing) failure rate can be inferred. When curve embraces diagonal line a constant failure rate can be assumed. Let t₁, t₂.  . . t_n be the n failure times of an equipment with suspensions between two few successive failure times. If all the units are put into test at the same time, then the total test time TTT_i for all units at time t_i is defined as,

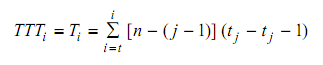
which is equivalent to the cumulative time up to the end of ti for, i = 1,2, . . . , n where

t₀=0. This is shown pictorially in following Figure The plot of CDF (which is equal to i/n) versus normalised TTT value (TTT_i/  TTT_n) is the TTT plot.

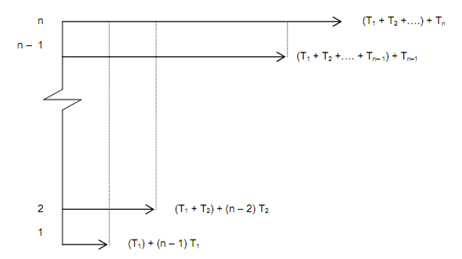
                                                               Figure: Total Time on Test Calculation

When the sample size 'n' increases to infinity the TTT plot converges to a life distribution F (t) from which the sample has come and it is the TTT transform. If t_n is not the last observed failure, then a pseudo time or last censored time after last failure, t_{n + 1} is defined as,

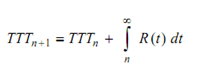
and the scaled TTT is, φ_i  = TTT_i  /TTT _{n +1}