BH Magnetization Curve:
The BH Magnetization Curve in Figure shows how much flux density (B) results from increasing the H flux intensity. The curves in Figure are for two kinds of soft iron cores plotted for typical values. A curve for soft iron 1 display in which flux density B increases rapidly along with an increase in flux intensity H previous to the core saturates, or develops a "knee." After that, an increase in flux intensity H has little or no effect on flux density B. A Soft iron 2 requires a much larger increase in flux intensity H before it reaches its saturation level at H = 5000 At/m, B =0.3 T.
Air, that is nonmagnetic, has an extremely low BH profile, as shown in Figure.
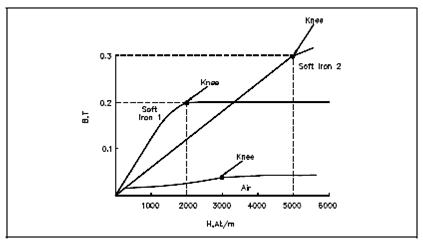
Figure: Typical BH Curve for Two Types of Soft Iron
The permeability (µ) of a magnetic material is the ratio of B to H. Equation (1-18) is the mathematical representation for magnetic material permeability.
µ = B / H (1-18)
The average value of permeability is measured where the saturation point, or knee, is first established. The above Figure shows that the normal or average permeability for the two irons as follows.
µ soft iron 1 = B/ H = 0.2/2000 = 1 x 10-4 (T m)/At
µ soft iron 2 = B/ H = 0.3/5000 = 6 x 10-5 (T m)/At
In SI units, the permeability of a vacuum is µ0 = 4Π x 10-7 H/m or 1.26 x 10-6 or T-m/At. In sequence to calculate permeability, the value of associative permeability µr must be multiplied by µo. Equation (1-18) is the mathematical representation for permeability.
µ = µr x µo (1-18)
Example: Find out the permeability of a material that has a relative permeability of 100.
µ = µr x µo = 100 (1.26 x 10-6)
= 126 x 10-6 (T- m) /At