Mathematical Representation:

Let us assume that there are only two firms in the industry.

The market demand function is given by, P = a - b(X); X = X₁ + X₂ where X₁ and X₂ are the output of firm 1 and 2 respectively.  
The cost functions of the two firms are given by C1 = f1(X₁) and C₂ = f₂(X₂) respectively and C₁ < C₂.

The leader (firm 1, as it is the low cost one) assumes that the rival firm would produce an equal amount of output such that X₁ = X₂

Therefore, the demand function of the leader becomes P = a - 2b(X₁)

The profit function of the low cost leader is given by:

Π₁ = PX₁ -C₁ =(a - 2bX₁) X₁ - C₁

Differentiating partially with respect to X1  and setting the derivative equal to zero yields,

∂Π₁/∂X₁ = a - 4bX₁ - ∂C₁/∂X₁ = 0  
or, a - 4bX₁ = ∂C₁/∂X₁  
i.e., MR = MC

Solving this equation, we get the equilibrium value of X1, after checking for the second order condition that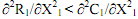

From the demand function, we can find out the equilibrium price level of the firm. The follower firm will accept the equilibrium price achieved by the leader.