Reduced Lottery:

Every compound lottery can be presented as a reduced  lottery which is same as that of the simple lottery where the consequences, as depicted in the above example, you receive either Rs.2, Rs.4 or 0 with probability 1/2  ,  1/4 and 1/4. To appreciate the logic, you can present this example in terms of a decision tree.  

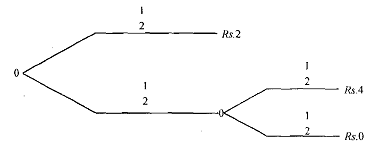
From  the decision tree,  you  can get  the  reduced  form probabilities. The probabilities of  the  second lottery  with  prizes  Rs.4  and  0  are obtained multiplying probabilities associated  with  each node,  viz.,  (1/2 x 1/2)  and (1/2 x 1/2)

To see why  compound lottery can be presented  as a simple lottery, you may consider a situation where an individual is not sure, which of the lotteries, L = 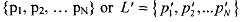, she is facing. So she assigns probability α to it being  L  and  (1 - α) to  it  being L'  . Now,  consider the resulting compound lottery

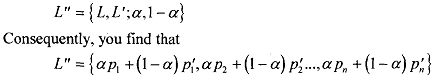
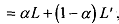which  is a simple lottery. Thus, a compound lottery is an average of simple lotteries.

So, for  any  compound  lottery 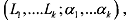, we  can  calculate a corresponding reduced  lottery as a simple lottery L =  (p₁, . . .  p_n)  that generates the same ultimate distribution over outcomes. Taking probability of outcome n in the reduced lottery is 

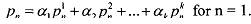
That  is,  you  simply  add  up  the probabilities  p_n^k  of  each outcome  n  in  all lotteries, k. multiplying each p_n^k by the probability  α_k of each lottery k.