Calculate the effective area and effective moment of inertia:

Calculate the effective area and effective moment of inertia of the composite column section shown in Figure 3 composed of welded flange and web plates. The web plate is 6 mm and the flange plates are 8 mm in thickness. The column has an effective length of 3.4 m (f_y = 250 MPa). Find the slenderness ratio of the column.

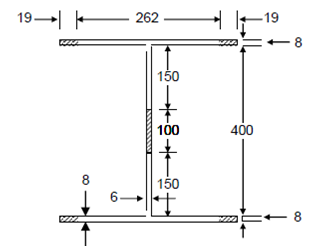
Figure

Solution

For the flange plate, b/t = 256/√ f _y =256/√250 = 16.2 (maximum is 16 t)

Hence, maximum allowable flange projection = 16 × 8 = 128 mm

Actual flange projection = (300 - 6)/2 = 147 mm

∴ Length to be ignored on each end = 147 - 128 = 19 mm

(Shown shaded in the Figure 6.3).

For the web plate, b/t = 1440/√ f_y =1440/√250 = 91.1

(Maximum allowed is 90 t)

Hence maximum allowed web depth = 90 × 6 = 540 mm

Which is greater than the actual web depth of 400 mm ∴         OK.

However, maximum permissible b/t ratio for the web is

800/√ f_y = 50.6 (maximum 50 t)

Hence, effective depth = 50 × 6 = 300 mm

∴ The excess depth to be ignored = 400 - 300 = 100 mm and is situated centrally as shown shaded in Figure 3.

The effective area of the section is

(300 - 19 × 2) × 8 × 2 + (400 - 100) × 6 = 5992 mm²

It must be remembered that all the geometrical properties, e.g. moments of inertia, radii of gyration, slenderness ratio, etc. in the section that are modified accordingly.

For example, in the composite section of Example 6.1 above, we have moment of inertia

I_XX =[262x8³/12 + 262x8x204²] x2 +[6x400³/12 - 6x 100³/12]

= 205,976,629 mm⁴

Similarly,       I_YY = 8 × (262)³/12 x2 + 300x6³/12 = 23, 985, 037 mm⁴

∴          r_xx 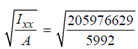 = = 185.4 mm

r_yy  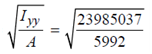=  = 63.3 mm

The least radius of gyration = 63.3 mm and the slenderness ratio of the column

λ = l/ r_min = 3400/63.3 = 53.7