Correcting Observed Bearings

In a compass if local attraction is detected survey observed bearings can be corrected by any one of the following two methods:

Method I: It can be noted that by local attraction the included angle is not influenced as both readings are equally affected. Therefore, first calculate included angles at each station, commencing from unaffected line and using included angles, the corrected bearings of all lines can be calculated.

Method II: In this method, due to local attraction errors at each of the affected station is found beginning from the bearing of a unaffected local attraction, the bearing of the successive lines are adjusted.

With the below examples these methods are illustrated:

Example: the following bearings were observed, with a compass in a closed traverse. Calculate their interior angles and then compute the corrected magnetic bearings:

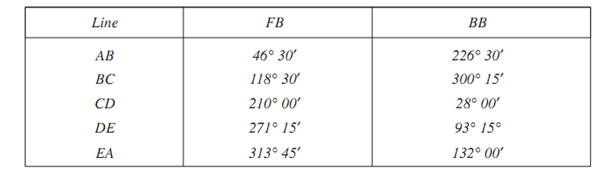
Solution: Given figure shows the traverse. Difference between FB and BB of line AB is accurately 180°. Therefore, by local attractions stations A and B are not affected. Therefore, all the bearings taken from stations A and B are correct magnetic bearings.

Correct bearing of AB = 46° 30′

Correct bearing of BA = 226° 30′

From the figure,

∠A = 132° 00′ - 46° 30′ = 85° 30′

∠B = 226° 30′ - 118° 30′ = 108° 00′

∠C = 300° 15′ - 210° 00′ = 90° 15′

∠D = (360° - 271° 15′) + 28° 00′ = 116° 45′

∠E = (360° 00′ - 313° 45′) + 93° 15′ = 139° 30′

Total Interior Angle           = ∠A + ∠B + ∠C + ∠D + ∠E

                                                = 540° 00′

 So there is no observations error.

[Note: In a pentagon sum of interior angles = (2n - 4) × 90 = (2 × 5 - 4) × 90 = 540°. it is to be distributed equally to all interior angles If there is observation error].

Since, by local attraction stations A and B are not affected, correct bearings are: Bearing of AB  = 46° 30′

Bearing of BA  = 46° 30′ + 180° 00′ = 226° 30′

Bearing of BC  = 226° 30′ - ∠B = 226° 30′ - 108° 00′ = 118° 30′

Bearing of CB  = 118° 30′ + 180° 00′ = 298° 30′

Bearing of CD   = 298° 30′ - ∠C = 298° 30′ - 90° 15′ = 208° 15′

Bearing of DC   = 208° 15′ - 180° 00′ = 28° 15′

Bearing of DE  = 28° 15′ - ∠D = 28° 15′ - 116° 45′

= - 89° 30′ = - 88° 30′ + 360° 00′ = 271° 30′

Bearing of ED  = 271° 30′ - 180° 00′ = 91° 30′

Bearing of EA  = 91° 30′ - ∠E = 90° 30′ - 139° 30′

= - 48° 00′ = - 48° 00′ + 360° = 312° 00′

Bearing of AE  = 312° 00′ - 180° 00′ = 132° 00′

[Checked. It should be equal to the observed bearing, as station E is not affected].