Chebyshev's Lemma:

Let X be a random variable with mean μ and variance σ². Then Chebyshev's lemma states that for any k > 0

P{¦X-μ¦≥ k} ≤ σ²/k²

Proof:

Let X be a continuous random variable with pdf f ( x ). We have

σ² = Var (X) = 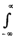(x-μ)² f(x)dx

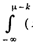= (x-μ)² f(x)dx + 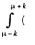(x-μ)² f(x)dx

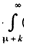+ (x-μ)² f(x)dx ≥  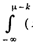(x-μ)² f(x)dx + 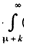(x-μ)² f(x)dx

≥ k² {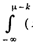 f(x) dx + 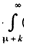f(x) dx}

since in both the ranges of integration ( x - μ )² ≥ k².

Hence

σ ² ≥ k² P(X ≤ μ - k ) u X ≥ μ +k) =k² p(¦X- μ¦≥ k)

or

P(¦X-μ¦≥ k) ≤ σ²/k²

The inequality can also be proved by taking X to be a discrete random variable.