Open Belt Drive:

The open belt drive is illustrated in Figure. Assume O₁ and O₂ are the pulley centers and AB and CD are the common tangents on the circles demonstrating the two pulleys. The entirety length of the belt 'L' is given by following

L = AB + Arc BHD + DC + Arc CGA

Assume r be the radius of the smaller pulley,

R be the radius of the larger pulley,

C be the centre distance among the pulleys, and

β be the angle subtended through the tangents AB and CD with O₁ O₂.

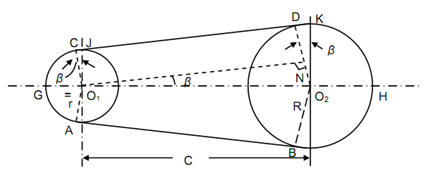
Draw O₁ N parallel to CD to meet O₂ D at N.

By geometry,  ∠ O₂ O₁, N = ∠ C O₁ J = ∠ D O₂ K= β

Arc BHD = (π + 2β) R,

Arc CGA = (π + 2β) r

AB = CD = O₁ N = O₁ O₂ cos β = C cos β

sin β= R - r/ C

or,

 β= sin ^-1  (R - r )/ C

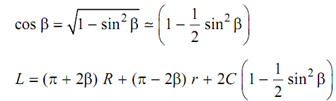
For small value of β;

        β= (R - r )/C

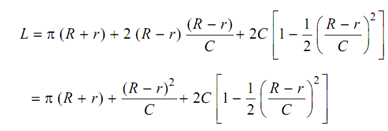
It provides approximate length.