Semi-elliptic Type Leaf Springs:

Figure illustrate a carriage spring carrying a central load W.

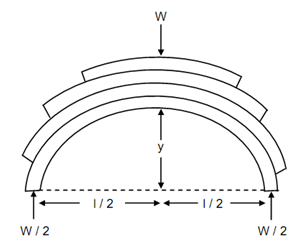
Figure

b = Width of leaves,

t = Thickness of leaves,

W = Load,

y = Rise of crown,

n = Number of plates, and

R = Initial radius of curvature of plates.

Section modulus of single plate =       bt ² / 6

Z for the whole spring =  nb t ²/6      

Maximum BM,

M  = Wl  /4

M  = σb . Z

σ_b  = M/Z = (wl/4)/ n (bt²/4) = (3/2) .(  Wl / nbt ²)

From geometry of circles, because each of leaf is supposed to be bent in form of a part of a circle.

y (2R - y) = (l /2)× (l/2)

∴          y =  l₂ / 8R

M/ E I  = 1 / R -  1/ R₀

 ⇒        (- Wl /4)/ E . (nbt 3/12) = 8/l² ( y - y₀ )

∴ Deflection,

Δ= 3W l³ / 8 nbt ³ E

U =       (1/2) W Δ =3W ² l ³/16 nbt ³ E

Spring constant

 = W/ Δ  = 8 E nbt³ / 3l ³

Proof Load : Load needed to make the spring flat.