Theoretical estimates

Theoretical lattice energies can be measured if some interaction potential between ions is specified. The most significant term in the ionic model is the long-range Coulomb interaction among charges. A complex summation is essential over the distinct pairs of like and unlike charges appearing at distinct distances in the crystal structure and provides the Coulomb energy per mole of lattice as

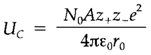
In which N₀ is Avogadro's constant, z₊e and z_-e are the charges on the ions and r₀ is the distance among them and A is the Madelung constant coming from the long-range summation of ionic interactions. A relies on the structure and increases slowly with the coordination number. (For instance, values for the simple AB structures are: zinc blende (CN=4) 1.638; rocksalt (CN=6) 1.748; CsCl (CN=8) 1.763.)

The attractive Coulomb energy requires to be balanced against the contribution from the short-range repulsive forces that take place between ions when their closed shells overlap. There is no correct simple expression for this repulsion. In the Born-Landé model it is supposed proportional to 1/rⁿ, in which n is a constant that changes in the range 7-12 depending on the ions. The resultant expression for the lattice energy is

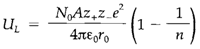
The Born-Mayer equation is a different (and possibly more correct) form based on the assumption of an exponential form for the repulsive energy. Both equations expect lattice energies for compounds like alkali halides that are in reasonably close agreement with the 'experimental' values from the Born-Haber cycle. Some instances are displayed in Table 1. A strict comparison needs some corrections. Born-Haber values are usually enthalpies, not total energies, and are estimated from data generally measured at 298 K not absolute zero; additional corrections can be made, for instance, including van der Waals' forces among ions. When these expanded calculations are compared with experiment several compounds agree well (see Table 1). Important deviations do take place, though; for instance, in compounds of metals in later groups where bonding is surely less ionic (example AgCl).

Table 1. Comparison of lattice energies (all kJ mol^-1) determined by different methods

One of the drawbacks of the fully theoretical approach is that it is essential to know the crystal structure and the interionic distances to estimate the lattice energy. The Kapustinskii equations conquer this limitation by making some suppositions. The Madelung constant A and the repulsive parameter n are put equivalent to average values and it is also assumed that the interionic distance can be approximate as the sum of anion and cation radii r₊ and r_-. The simple of the Kapustinskii equations for a binary solid is

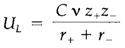
ν is the number of ions in the formula unit (example two for NaCl, 3 for MgF₂ and five for Al₂O₃) and C is a constant equivalent to 1.079×10⁵ when U_L is in kJ mol^-1 and the radii are in pm. The Kapustinskii equation is helpful for rough calculations or where the crystal structure is not known. It emphasizes two necessary characteristics of lattice energies, that are true even when the bonding is not fully ionic:

1. lattice energies raise strongly with increasing charge on the ions;
2. lattice energies are all the time larger for smaller ions.

Calculations can be expanded to complex ions like carbonate and sulfate by the make use of thermochemical radii, chosen to provide the best match among experimental lattice energies and those estimated by the Kapustinskii equation.