Continuous culture

A stirred tank reactor regulated for temperature, pH, and oxygen so that all conditions remain constant can be adapted to a continuous mode of action. If the continuous culture grows so that it is limited by one of the medium components it is called a chemostat in Figure but limitations on biomass (turbidostat) or electron potential (potentiostat)

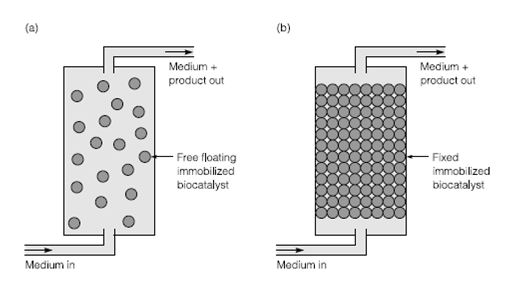
                                                  Figure . (a) Fluidized  and  (b) fixed bed bioreactors.

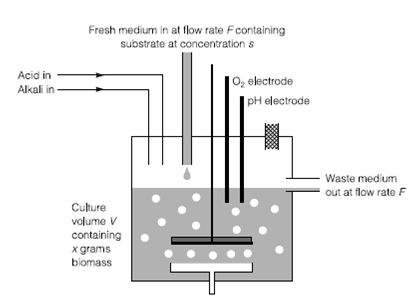
Figure  4.  The chemostat. Temperature, pH, and oxygen control are omitted for clarity. x = biomass concentrations; s = growth-limiting nutrient concentration; F = flow rate of culture; V = volume.

can be imposed. In an industrial context, continuous culture is useful as it provides a constant production of biomaterials for downstream applications. In the research laboratory, the kinetics of the chemostat provides additional insight into the biochemistry and physiology of pure and mixed cultures.We assume that the action of the impeller means that the medium coming into the culture vessel is mixed instantaneously. This is known as the replacement time tr the time for one complete volume change of the vessel.

If V is the volume of the reactor and F is the flow rate:

                                                t_r  = V/F

If the flow rate is too high the organism cannot divide quickly enough to maintain growth in the vessel and eventually is diluted away washout. The flow rate can be adjusted so that the rate of washout of biomass equals the maximum growth rate mm. At this point any change in substrate concentration will have a direct effect on biomass. The group of conditions under which biomass remains constant over several volume changes of the chemostat is known as a steady state.

The specific growth rate of a chemostat culture is equal to the dilution rate, D

                                               D = F/V

This is always the case as the net increase in biomass equals growth minus output. Over an infinitely small period this becomes:

                                         V.dx = V.x.dt - Fx.dt

                                    Dividing throughout by V.dt

                                        dx/dt  = (m - D)x

 So at the steady state when dx/dt = 0, then m = D.

We can also calculate the biomass and growth-limiting substrate concentrations by rewriting the balance for the growth-limiting substrate (net increase in biomass = growth- output) for the case over an infinitely small period:

V.dx = F.s_r.dt - Fs - Vmx.dt/Y

where Y is the growth yield. Divide throughout by V.dt

ds/dt = D(s_r  - s) - mx/Y

In the steady state, dx/dt  = ds/dt = 0, then the  steady-state values  of x and  s (written as x~ and ~s ) are given by:

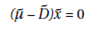
and

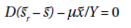
To obtain  x~ and ~s, we can use the equation for specific growth rate

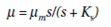
where Ks  is the  equivalent of the  Michaelis–Menten constant and  is inversely proportional to the affinity of the organism for the substrate. As m = D, then

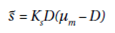
or

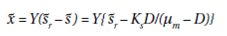
The  critical  dilution rate the  dilution rate  above in that the  culture begins to  wash- out  is obtained from  the  maximum growth rate  when s = sr. Inserting this  value  in m = mms/(s +Ks) results in:

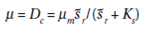
If sr is very much greater than K, then it follows from the above equation that Dc   is approximately equal to mm.