Splines:

It is a piecewise fit and therefore can be utilized if large amounts of accurate data are available. Spline functions consider small subsets of data and fit these with lower order polynomials. It is an important technique utilized in a wide range of applications. The interpolating polynomial can be quadratic, linear, cubic, etc.

            The cubic spline functions are the most extensively utilized. Considering two arbitrary points x_i and x_{i + 1} at which the function f (x) is to be determined

The cubic which passes through these points is taken as following

f_i (x) = a₀ + a₁ x_i + a₂ x²_i + a₃ x³_i ... for x between x _i and x _{i + 1}

Substituting x = x_i and x_{i + 1}, we contain, respectively

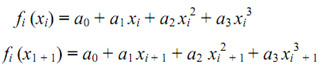
As there are 4 constants to be find out, other 2 conditions are obtained by using the continuity of first and second derivatives at x_i and x_{i + 1} (for smooth transition).

The cubic f_i (x) over x_i = x = x_{i +1} is attained as

f_i ( x) =  (f ′′( x) ( x_{i +1}  - x)³ /6Δ x_i  )+(( f ′′( x_{i +1} ) ( x - x_i )³)/6Δ x_i  )+

 {[f(x_i)/ Δ x_i  - [ (Δ x_i  f ′′( x_i ) )/6]} ( x_{i +1}  - x)+ {[ f ( x_{i +1} ) / Δ x_i  ]- [Δ x_i  f ′′( x_{i +1} )/6]} (x-x_i)

where, Δ x_i = x_{i + 1} - x