Example: Find out the voltages VAE & VEC in given circuit.
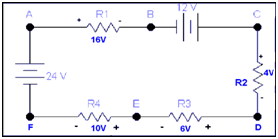
Solution: To solve the circuit we will draw some imaginary arrows across point A E & C.
The circuit might be redrawn like this
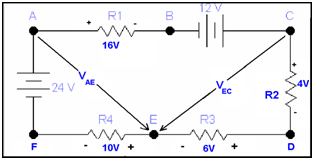
As points A & E as well as E & C are not physically close, we utilize the arrow notation.
Our approach to finding the unknown voltage is to apply KVL having the unknown voltage in the closed path, so to VAE we will utilize the path AEFA or ABCDEA.
The equation for two paths in which VVAE is the X known is
For path AEFA
VAE +10 - 24 = 0 ------------- (1)
VAE = 14 V
Now for path ABCDEA
16 - 12 +4 +6 - VAE =0 ------------- (2)
VAE = 14 V
By solving both loops i.e. AEFA & ABCDEA we will obtain VAE = 14 V.
We will calculate VEC utilizing paths CDEC or CEFABC. The value of VAE is also known therefore we can also utilize path CEABC.
By applying KVL for each the paths
For the path or loop CDEC
4 + 6 - VEC= 0 ------------- (A)
VEC = 10 V
For the path or loop CEABC
+VEC + VEA +16 - 12 = 0 ------------ (1)
In above calculated equation (1) VEA= -VAE
+VEC - VAE +16 - 12 = 0 ------------ (B)
For the path or loop CEFABC
+VEC +10 - 24 + 16 - 12 =0 ------------ (C)
By solving each of three equations we get
VEC = 10 V