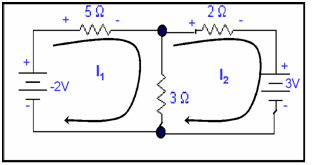
Q:  Determine the power dissipated by 3Ω resistance.

Solution:

            We may write I₃=I₁-I₂, I₁ & I₂ are opposite to each other so they will cancel  each other up to some extent to give I₃.this is given in the circuit that direction of I₁ is in clock wise direction whereas I₂ is also in clockwise direction.

We imagine that voltage V_x for mesh 1 & V_y for mesh 2 across the 3 ohm resistance.

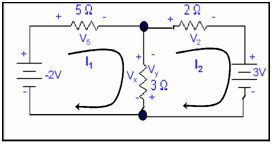
            For mesh 1

                                               -(-2)+ V₅ +V_x=0

                                                            Also from applying Ohm's law

                                                V₅ = 5 I₁ & Vx=3 ( I₁ - I₂ )

                                                   2+5I₁+3(I₁-I₂) = 0

                        Or                               8I₁-3I₂ = 2 ........(1)

             Now for mesh 2

                                                3( I₂ - I₁ ) + 2 I₂ + 3 = 0

                        Or                                - 3I₁ + 5I₂ = -3 ...........(2)

                        By Solving two mesh equations (1) &  (2), we obtain

                                                I₁ = - 612.9 mA

                                                I₂ = - 967.7 mA

                                                            I₃=354.8 mA

                        Therefore

                                    Power = 3 (354.8)2

                                                 =377.7 mW

                        It does not matter whether we write I1-I2 or I2-I1 due to square term.

Now by using nodal analysis

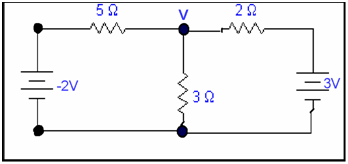
                                    0 = (V-(-2)/5) + (V/3) + (V-3)/2)

                                               V = 1.065Volts

                                    Power = | (V₂/R) =378.1 mW