Applying Kirchhoff's Voltage Law:

To a simple series circuit, Kirchhoff's voltage law corresponds to Ohm's Law.   To find out the current in a circuit show in the Figure through using Kirchhoff's voltage law, use equation (2-15).

∑E _source =  ∑IR                 (2-15)

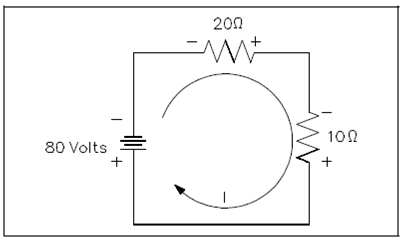
Figure: Using Kirchhoff's Voltage Law to find Current with one Source

80 = 20(I) + 10(I)

80 = 30(I)

I = 80/30 = 2.66 amperes

In the given problem above, the direction of current flow was known before solving the problem. While there is more than one voltage source, the direction of current flow might or might not be known.  Within that case, a direction of current flow must be supposed in the starting of the problem.  All the sources which would aid the current in the supposed direction of current flow are then positive, and all which would oppose current flow are negative.  If the supposed direction is right, the answer will be positive.  If the direction assumed was wrong the answer would be negative.  Within any case, the correct magnitude will be attained.

For example, what is the current flow in Figure 34?  Assume that the current is flowing in the direction shown.

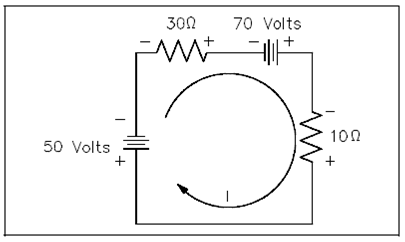
Figure: Using Kirchhoff's Voltage Law to find Current with Multiple Battery Sources

Using Kirchhoff's Voltage Law:

∑E_source = ∑IR

50-70 = 30 I + 10 I

-20 = 40 I

I = -20/40

I = -0.5

The result is negative.  The current is in fact 0.5 ampere in the opposite direction to that of the supposed direction.