Rigid Bodies in Plane Motion:

We know that plane motion of a rigid body is the combination of motion of translation and motion of rotation. The dynamic equilibrium equations developed for translation motion and rotational motion may be applied simultaneously to the body undergoing plane motion.

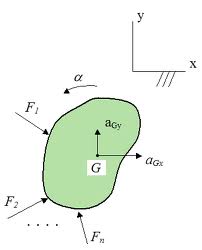
Let C be the mass centre of a body which moves parallel to xy plane under the action of applied forces, and let A be any particle of mass dm at the distance r from an axis through C, normal to the plane of motion. Let x_c , y_c be the coordinates of point C which is also considered as a pole and θ the angle that AC makes with the x axis. These three coordinates define completely the position of the body at any instant t. New we may imagine the point A as having two types of motion:

(i)         translation together with the pole C, and

(ii)        rotation about the axis through C normal to the plane of motion.

Let us further assume that ax and ay be x and y directional acceleration components due to motion of translation. Also ω and α be angular velocity and angular acceleration of the body when it undergoes motion of rotation.