Mass Moment of Inertia:

Let us consider a rigid body K situated at a distance from an arbitrarily chosen axis u as shown in Figure the body may be considered as composed of infinite number of particles each of elementary mass dm. The total mass of the body can be written as m = ∑ d m . Let any particle k of this body of mass dm situated at a distance of a_k  (perpendicular) from the axis u. Then the product ( a_k)² dm  with reference to every particle  (for all the particles in the body) assumes importance. The mass moment of inertia I_u of the body about u axis is now defined as the sum of all such products, (a_k) dm , taken over the entire body.

 Figure 7.1

So we have,

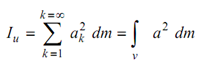 ------------- (1)

 If the body is homogeneous and continuous, the summation sign may be replaced by an integral sign as shown in Eq. (1). We should remember that the integration is to be performed over the entire volume of the body. The dimensions of moment of inertia shall be (mass) × (length)², so that it shall be measured in units of kg m².

The radius of gyration (k_u) is defined as :

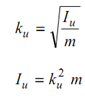                 ----------- (2)

The dimensions of radius of gyration shall be (length)¹, so that it may be measured in terms of m or cm units.