Representation of Kinetics of a Particle:

Newton's law of universal gravitation states that any two particles of masses m₁ and m₂ separated by a distance r attract each other with equal opposite forces that are directed from either particle towards the other. The magnitude of each pair of action and reaction forces is given by:

                                       F = G m₁ m₂ /r ²

where, G is the universal constant of gravitation. Now the value of G accepted is

G = 6.67 × 10^-11  N m ² / kg ²                                      ---------- (1)

We must understand that Newton's law of gravitation does not define any of the physical quantities (force, mass, length etc). However, Newton's second law defines the relations among these physical quantities. Here we try to describe the term weight, which is the gravitational force of attraction exerted on the body by the earth. The weight of a body depends upon its position relative to the centre of the earth.

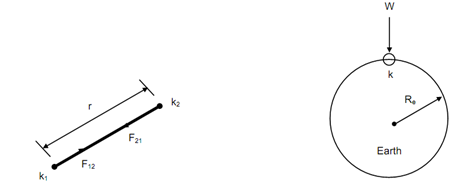
If m₁ and m₂ are the masses of two particles k₁ and k₂ at a distance r apart as shown in Figure (a), then they attract each other with forces F₁₂ and F₂₁ whose magnitude is defined by :

F₁₂  = F₂₁  = G m₁ m₂ /r ²

where, G is the gravitational constant.

Also we have

F₁₂  = - F₂₁  (Vectorially)

Figure (b) shows a body of mass m on the earth's surface. M is the mass of the earth and, R_e is its radius. The gravitational force, W, exerted by the earth on this body shall be

W = GMm/(R_e)² = mg

where,

g =GM/(R_e)²

(a)                                                                                   (b)

Figure

The body shall exert a force of equal magnitude on the earth which shall have a negligible effect on earth, considering the very large mass of the earth.

If we substitute M = mass of earth = 5.98 × 10²⁴  kg, R_e  = 6378 km,

G = 6.67 × 10^-11 N m ² / kg ² , then g = 9.81 m / sec ² . The actual value of g varies from point to point due to variations in the earth's radius and density. In engineering particle it is sufficient to assume that

                                       g = 9.81 m / sec ²  = 981 cm / sec ² .

The prerequisites for understanding the fundamentals of such analyser are the concept of a particle, a rigid body, kinematics of a particle and that of a rigid body.