D′Alembert's Principle - Application to a Particle:

By the use of this principle, difficult problems of dynamics can be reduced to simpler problems of statics.

Consider a particle P illustrates in Figure (a). A force F is acting upon this particle. The acceleration of the particle can be attained by the equation:

                                                             F = ma

where, m is the mass of the particle in which F produces on acceleration a. This equation can be written as

                                            F - ma = 0           or                 F + F_i  = 0

where, vector F_i  = - ma is termed as inertia force, and it is always directed opposite to the acceleration a of the particle (Figure

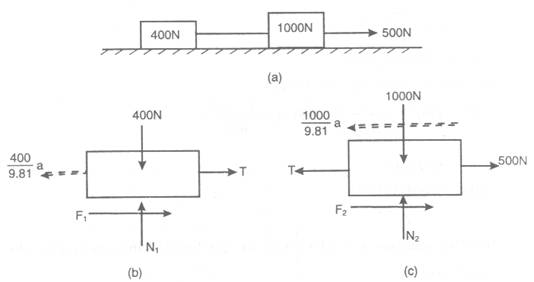
This also may be described as discussed below :

A force F is acting on a particle P, and inertia force F_i = - ma is imagined to be also acting on the particle. Then F and F_i are in equilibrium. It is known as D'Alembert's principle.

When F and F_i act on a particle, the same shall remain in equilibrium. To distinguish this equilibrium from static equilibrium it is termed as dynamic equilibrium.

When a number of forces are acting on the particle, the principle can be applied as discussed below. Let F₁ , F₂ , . . . , F_n be the forces acting on a particle P as illustrated in Figure (a). We may calculate the resultant force R of the system. Then we may write R = ma, where a shall give the resultant acceleration of the particle.

This equation may be written as

 R - m a = 0     or R + F_i  = 0

where, F_i  = - m a is the inertia force.