Velocity of Points in a Rigid Body:

We consider the equation of pole A in the body as

r_A (t ) = x A (t ) i¯ + y _A (t ) j¯

 At any instant position vector of any other point B is provided by :

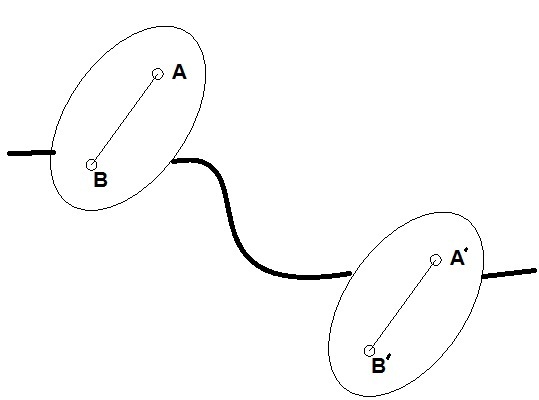
r_B  = r_A  + r_AB

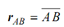  is a vector of constant magnitude because distance AB is constant. But

the direction of this vector can change with respect to time so that d r_AB/ d t does exist.

Then by differentiating, we obtain

v_B = d r_B/dt       = d r_A/  dt + d r_AB /dt

= v _A  + d r_AB/ d t

d r_AB / d t  is the differentiation of a vector of constant magnitude but altering in direction. If ω is the angular velocity with which the body rotates about the axis, then we may write

                                                d r_AB /dt = ω r_AB

This is a vector v _AB of magnitude ω. r_AB , acting at right angles to AB.

Then                                v _B = v _A + v _AB

Here, in this equation, we should note that velocity of B consists of two components.

(a)        The component v _A which represents the velocity of translation of pole A.

 (b)       The component v _AB of magnitude ω r_AB  is caused by the rotation of point B about an axis passing through A, perpendicular to the plane XOY. This component shall be perpendicular to AB.

                                                           v _B  = v _A  + ω × r_AB