Velocity and Acceleration of a Point in a Rotating Body:

The velocity and acceleration of any point P may be expressed in terms of angular velocity and angular acceleration.

Referring to Figure (a), let the position vector of the point P be r (t). As the body rotates P shall trace out a circle of radius a in a plane parallel to XOY plane, where a = r sin θ. The centre C of the circle will be along z-axis. The path of P is illustrated separately in Figure (b) for better visualization. P_o is the starting point and distances s = a φ is measured from P_o.

Then linear velocity of P can be obtained by

v = ds/ dt =  d /dt (a φ) = a dφ/ dt  = a ω

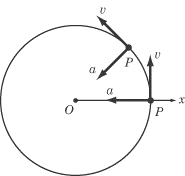
This will be directed along the tangent to the circle at P. The magnitude of velocity v is proportional to the distance of P from the centre of its path.

The acceleration of point P can be obtained as shown in Figure. We know that P moves along a circular path of radius a. the acceleration of P will have two components, viz tangential component and normal component.

Therefore, we have

a = a_t  + a_n

= dv /dt t^ +( v²/a )n^

But       v = a ω

∴ dv/ dt = a dω/ dt = a α

∴ a = a α t^ + (a ²  ω² / a ) n^

∴ a = a α t^ + a ω² n^

Magnitude

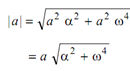
If β is the angle the resultant acceleration makes with normal component, then

tan β = a_t / a_n  =  α/ ω²