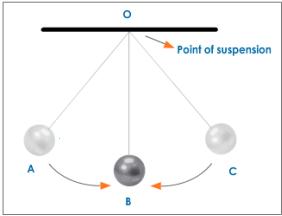
Translatory Motion:

While a rigid body moves in plane in such a manner that a straight line in the body remains parallel to itself, such motion of the body is called as the motion of translation.

Line AB moves parallel to itself at all the times, such that at different instants it suppose the positions A₁ B₁, A₂ B₂ etc. The vector

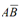= rAB remains constant during the motion, since the magnitude & direction of this vector does not change. Let two wheels A and B and a bar PQ hinged at both ends to these wheels. When the wheels rotate about their respective axes, the bar PQ will undergo motion of translation. The position P′Q′ , at any instant, of the bar shall be parallel to its original position PQ given in Figure

We may write down the equation of position vector at B as follows.

r_B  = r_A  + r_AB

Differentiating this equation with respect to time, we obtain

dr_B /dt = dr_A /dt + dr_AB /dt

But vector r_AB  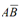= is constant in magnitude and direction.

∴ dr_AB / dt=0

but

dr_A /dt = v _A  and  dr_B /dt = v_B

or         v _B  = v _A

Differentiating once again, we obtain

d 2 rB/dt² = d ² r_A /dt     or       a_B = a _A

We also keep in mind that A and B are particular two points in the rigid body. Thus, we may say that the velocities and accelerations of all points in the rigid body undergoing motion of translation are the same at all instants.