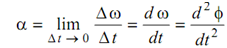Rotation of a Rigid Body about a Fixed Axis:

Consider a body which rotates about z axis as shown in Figure 5.26. Any point P lying in the XOY plane will move along a circular path as shown. Point Q will similarly trace out a circle in plane parallel to XOY plane.

A plane OA passes through the axis of rotation OZ which will be assumed to be fixed to the body such that it rotates with the body. At any instant t, the position of the body can be defined by the angle this rotating plane makes in space with a plane fixed. This angle is φ as shown in Figure. This is also called angular displacement. This angle φ changes as time changes, and φ will be a function of time.

                                                                            ∴ φ = φ (t ).

After a small time interval Δt, the plane OA rotates further and occupies the position OA′. Angle φ shall alter by the amount Δ φ = angle POP′.

Then

 Δ φ / Δ t = average angular velocity and if ω = instantaneous angular velocity, so

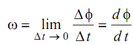
We should note that angle φ is measured in radians and the units of ω will be radians/second also written as sec^{- 1}.

If the body undergoes N number of revolutions per minute, then we get

                          ω = 2 π N /60 radians / second.

Further, we may define instantaneous angular acceleration α as below