Plane Motion of a Rigid Body:

While the body moves in such a way that all the points in the body move parallel to a fixed reference plane, such a motion of the body is called as the plane motion.

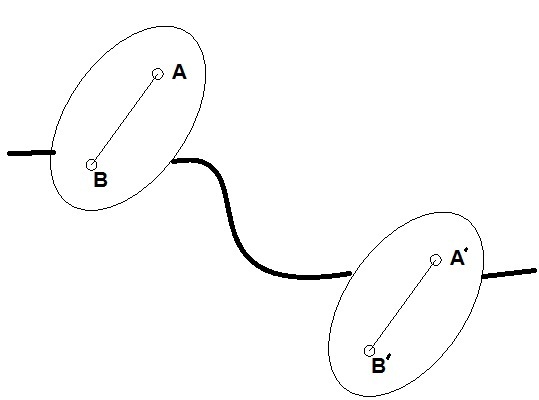
Let a section of the body 's' as illustrated in Figure on XOY plane. Consider the point A as pole and x_A and y_A as coordinates of the point. After sometimes s will move and occupy positions s′ such that line AB occupies the position A′ B′. The paths AA′ and BB′ traced by A and B shall be different.

We may write coordinates of B as :

                     x_B  = x _A  + a cos φ

and            y _B  = y _A  + a sin φ

The displacement of a body undergoing plane motion is equal to a translation of a pole and a rotation w.r.t. an axis passing through this side.

The final position of AB defined as A′ B′ may be considered as discussed below. First, let the body occupy the position A′ B′ such that the particles have motion of translation, i.e. they move parallel to AB.

Then we imagine that the body rotates about an axis passing through A′ in the anticlockwise direction through an angle Δ φ such that point B″ occupies the position B′.

Also we can consider that the body has occupied first position of B′A″ and then rotated about an axis through B′ and occupied final position of A′.