Vector Representation of Motion:

If the motion of a particle is described by a position vector, then

r (t ) = x (t ) i¯ + y (t ) j¯ + z (t ) k¯ where i¯ , j¯ and k¯ are unit vectors along x, y and z-axes, respectively.

The direction cosines of this vector are cos α, cos β, cos γ. We have

                       r (t ) = x (t ) i¯ + y (t ) j¯ + z (t ) k¯

Then velocity

v = dr/ dt  = dx/ dt i¯ +dy/dt j¯ +            dz/dt k¯

∴ v = vx  i¯ + v y j¯ + vz  k¯

and

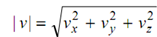
and

cos α = vx/v , cos β = v y/v , cos γ = vz/v

Likewise acceleration of the particle shall be obtained by

a = dv/dt = d2r/dt = d²x/dt i¯  +  d²y/dt j¯  + d²z/dt k¯

or         a = a_x i¯ + a _y  j¯ + a_z k¯

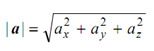
and

ax/a = cos α, a_y/a= cos β, a_z /a = cos γ