Linear Motion:

Consider a particle moving along x axis as shown in Figure, the displacement of this particle can be defined by its x-coordinate measured from fixed refimerence point O.

When the particle is on the right hand side of O, we can call this displacement positive, and when the particle is on the left hand side of O we can call the displacement negative.

As the particle moves, the displacement varies along time. If the displacement is x at any time t, the motion of the particle can be completely defined by the relation x = f (t), where f (t) stands for a function of time.

The relationship between x and t will based upon how the particle moves along x axis.

If          x = x₀  + v t

then constant x₀ represents an initial displacement at time t = 0, while the constant v represents the rate of increase of displacement. Such motion of a particle is called a uniform rectilinear motion.

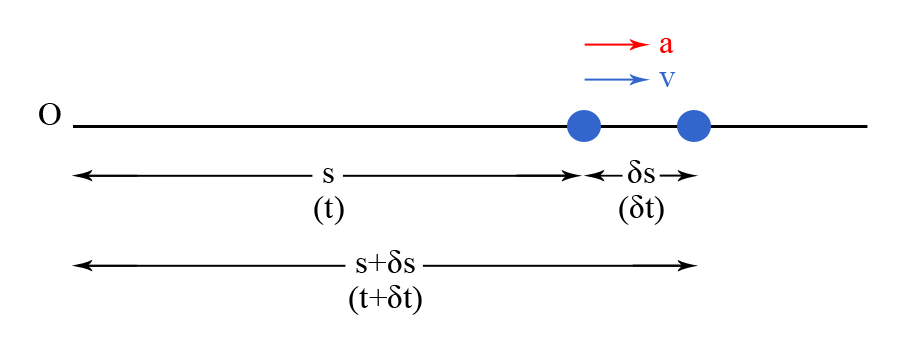
Consider a particle at A at time t as shown in Figure. After a small interval of time, Δt, the particle moves further and occupies position B such that

                                                              AB = Δ x

Then we may define,

                                       Δ x = Δ t

Average change of displacement, also called as average velocity during time interval Δt.

Δ x/ Δ t   as Δ t → 0 is called the instantaneous velocity which can be expressed as dx/ dt

Thus, mathematically the differentiation of x with respect to t gives us the instantaneous velocity.