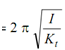Torsional Vibrations (Torsional Pendulum):

Let a circular disc of radius R associated to one end of a shaft of diameter d. The other end of the shaft is rigidly held. The axes OZ of the shaft pass through the center of the disc and are perpendicular to the plane of the disc. By applying external moment the body is turned about the vertical axis OZ or is twisted and then released.

Then the body performs oscillatory rotation about axis OZ which is known as torsional vibration

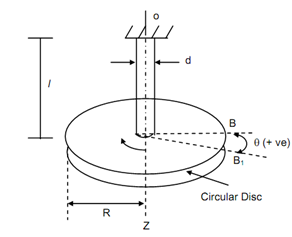
Assume θ be the angular displacement of any line AB, from the equilibrium position after time t.

The equation of motion may be written down as following

M = I d²θ/ dt ² = I  θ¨

 where, I is the moment of inertia of the disc w.r.t. the axis of rotation OZ and M is the moment w.r.t. the axis OZ of all the external forces acting on the disc.

The moment M is because of elastic reaction exerted by the shaft on the disc. The shaft may be thought to be a torsional spring of stiffness

K_t  = π d⁴ G/32 l

Where, G is modulus of rigidity of the shaft.

M  = - K _t  θ

I  θ¨ = - K_t  θ

θ¨ + (K_t/I) θ = 0

Comparing with the equation of simple harmonic motion,

Time period t =