Projectile:

A particle thrown up with some angle of elevation with initial velocity v_o shall traverse a path called trajectory, and the motion is called projectile as illustrated in Figure

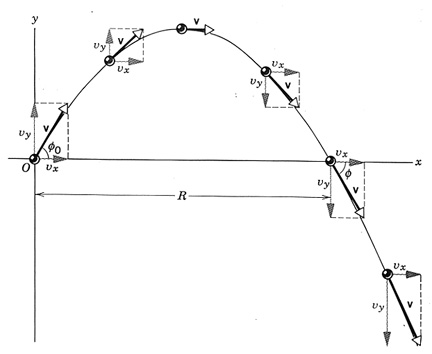
The equation of this motion may be written as under :

x = v₀  cos θ t

y = v₀ sin θ t - 1/2 gt ²

where, g = gravitational acceleration.

 Removing t from the above equations

t =        x / v_o  cos θ

y = x tan θ - g x² / 2 v ²  cos²  θ

Thus , It may be shown that the traced (trajectory) is a parabola. The velocity along x axis is constant and is equal to

                                              v_x  = v_o  cos θ

and      x = distance travelled along x axis

                                                                    = v_o  (cos θ) t

Velocity at any instant along y axis shall be

v _y  = v_o  sin θ - gt

and,     y = distance travelled along y axis

 = v_o sin θ t - (1/2) g t ²  (as written above)

H, the maximum height attained by the projectile, shall be attained at the instant when

v_y = 0.

∴ 0 = v _y  = v_o  sin θ - g t

∴ t = v_o  sin θ / g  = time since t = 0, to obtain maximum height (H).

Hence,

H = vo  sin θ × ((v_o  sin θ) /g)  - (½)g v_o²  sin² θ/g²

= v _o²  sin ²  θ / 2 g

While the particle crosses x axis again, that means when it is at B, vertical distance travelled is zero. It is called the range of the projectile and normally mention by R.

We have y = v_o sin θ t - (½) g t ²  = 0

then

∴ t = 2 v_o  sin θ / g

R = v_o  cos θ . t

= v _o   cos θ × ((2 v_o  sin θ)/g )= (v_o² sin 2 θ )/g

It gives us,

T = time for projectile = (2 v_o  sin θ )/g