Free Vibrations of Mass-Spring Systems:

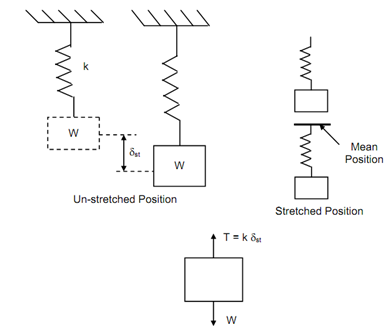
Let a body of weight W suspended from a spring of stiffness k and constrained to move in vertical direction. The spring has some unstretched length and extends by a length δ_st when weight W is suspended.

If the body is displaced from the location of static equilibrium and then released, it will move up and down around its mean position or will be free vibrating performing simple harmonic motion.

Figure

Let at any time't', 'x' be the displacement from the mean position.

Tension T in the spring = k (δ_{s × t} + x)

Writing down the equation of motion

(W/ g)  d ² x /dt ² = W - k (δ_{s × t}  + x)

δ_{s × t}  k = W

∴          (W/g)  d²x /dt²= W - W - k x = - k x

(W/g)  d²x /dt² + k x = 0

or,

 (W/g)  x¨ + k x = 0

x¨ + (k g/W) x =0

x¨ = - (k g/W) x =0

Comparing with the equation of simple harmonic motion,

ω ² =  k g/W      

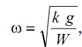
Time period,       t = 2 π/ ω ,

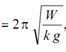
Therefore, the body vibrates with a time period find out as above.