Wrapping pairs:

Wrapping pairs comprise belts, chains & such other apparatus. Belt comes from one side of the pulley & moves over to other side.

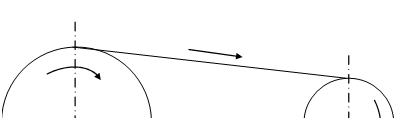
Wrapping Pair

 Resolve degrees of freedom for kinematic pairs illustrated in Figures (a), (b), (c) and (d) below :

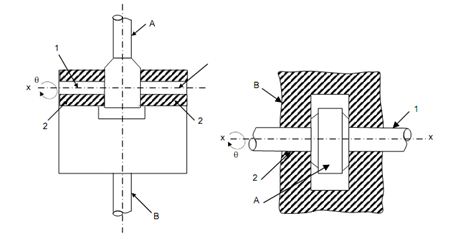
(a)                                                                        (b)

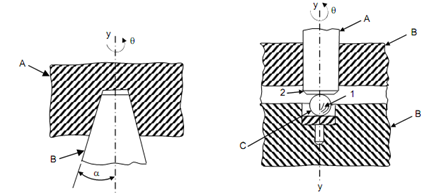
                          (c)                                                            (d)

Solution

 (1) In Figure (a), link A contain two round cylindrical turnnions 1 fitting into cylindrical holes 2 of link B. There is turning motion θ of link A w. r. t. link B around axis x-x. In this pair, link A contain relative turning motion w. r. t. axis x-x. Just one coordinate for rotation that is 'θ' is needed. Thus, this kinematic pair contains one degree of freedom

 (2) In Figure (b), link A is fixed on shaft (or pin) 1 & that fits in holes 2, in link B. There is just turning motion θ on link A w. r. t. link B, around axis x-x. Link A rotates in relation to link B. The relation motion is rotation of link A w. r. t. B and may be represented by a coordinate 'θ'. Thus, this kinematic pair contains one degree of freedom

 (3) In Figure (c), link A has internal conical surfaces along angle or taper α. Link B having the similar taper that fits into link A. There is rotary motion θ of link A w. r. t. link B. As illustrated in figure, the link A rotates w. r. t. B and it may be represented by a rotation coordinate 'θ'. Thus, this kinematic pair contains one degree of freedom.

(d) In Figure (d), link A is rotating around axis y-y and contain a flat end 2 resting on ball 1. The ball has freedom of movement in socket C of link B. There is turning motion θ around axis y-y of link A w. r. t. link B. Link A rotates on ball 1 that rests on a flat surface in link B. The relative motion of link A w. r. t. link B may be represented by a coordinate 'θ'. Thus, this kinematic pair contains one degree of freedom.