Find out all the instantaneous centres:

Find out all the instantaneous centres of a slider crank chain OAB illustrate in Figure and described how velocity of piston may be expressed in terms of crank speed?

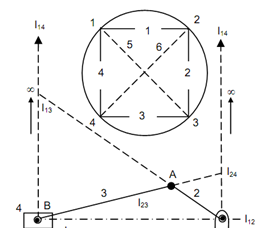
 DeterminaIt3i4on of Instantaneous CenOtres of Slider Crank Chain

Solution

No. of links = 4

∴

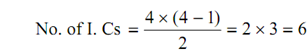
        Table of I. Cs

        I₁₂      I₁₃        I₁₄

                 I₂₃        I₂₄

                             I₃₄

Out of these six instantaneous centres, four I₁₂, I₂₃, I₃₄, I₁₄ may easily be situated at points O, A, B and infinity. As slider contain rectilinear motion, the instantaneous centre I₁₄ lies at infinity and line drawn perpendicular to its line of motion through any point will meet this point at infinity. To situate I₁₃ and I₂₄ circle diagram may be utilized.

As described in previous instance (Example 4.1), I₁₃ is represented through line joining points 1 & 3 in the circle. This line is common to triangles 1, 2, 3 & 1, 4, 3.

 Thus, two lines are drawn one joining I₁₂ & I₂₃ and second joining I₃₄ & I₁₄, i.e. line from I₃₄ perpendicular to OB. The pt of intersection of these lines is likewise, I₂₄ is achieved like point of intersection of the lines joining I₃₄ along I₂₃ and I₁₂ having I₁₄. The IC I₂₄ relates link 2 having link 4. While I₂₄ moves having link 2, the velocity of I₂₄ is provided by

                                    VI₂₄ = ω2  × I₂₄  I₁₂

 The direction is perpendicular to the line I₂₄ I₁₂. Now I₂₄ may be supposed to be moving having link 4. As velocity of all of the points in a link executing translation is similar thus, velocity of link 4, that means piston is given by VI₂₄ in direction and magnitude.