Determination of Instantaneous Centres in a Mechanism:

Kennedy's theorem may be utilized for determining all of the instantaneous centers in a mechanism. It can be verified with the help of some examples.

Example

In a four bar kinematic chain O₂A BO₄, link O₂O₄ is fixed. The length of links is as:

O₂A = 20 cm, AB = 45 cm, O₄B = 33 cm. O₂O₄ = 22 cm and ∠ O₄O₂A = 120^o

AC = 33 cm and O₄D = 21 cm

If crank O₂A rotates at 300 rpm in counter clockwise sense, locate all of the instantaneous centres and find out :

(1) angular velocity of link O₄B

(2) velocity of points C & D as illustrated in figure

Solution

Nos. of instantaneous centros,

N = (4 × 3 )/2= 6 .

     Table of I.Cs

I₁₂         I₁₃         I₁₄

            I₂₃         I₂₄

                        I₃₄

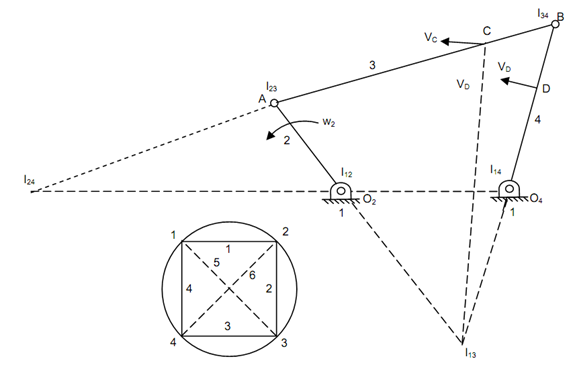
Since a first step, the configuration diagram is plotted by selecting appropriate scale.

Out of these 6 instantaneous centres four may be recognized easily by looking at the configuration diagram. These are I₁₂, I₂₃, I₃₄ & I₁₄ at points O₂, A, B & O₄ respectively. The left over two instantaneous centres I₁₃ and I₂₄ may be find out in a systematic manner by utilizing circle diagram. A circle of any arbitrary radius is drawn primary. All of the links are represented on this circle through equally spaced points at the circumference as illustrate in figure. On the circle the lines joining the points represent relative instantaneous centres. The lines that represent known instantaneous centres are drawn primary. For finding I₁₃, join points 1 & 3 in the configuration diagram. This line is common side to two triangles. Triangle 1, 2, 3 shows three instantaneous centres I₁₂, I₂₃ and I₁₃. Likewise, triangle 1, 3, 4 shows I₁₄, I₃₄ & I₁₃. According to Kennedy's theorem I₁₂, I₂₃ & I₁₃ must lie on a straight line. Also I₁₄, I₃₄ & I₁₃ must lie along a straight line. I₁₃ will be point of intersection of two lines drawn joining I₁₄ along I₃₄ and joining I₁₂ & I₂₃. A line joining I₁₂ & I₂₃ is drawn & another line joining I₁₄ and I₃₄ is also drawn. These two lines intersect at I₁₃ as illustrated in Figure. Now points 2 & 4 are joined. This line shows I₂₄. This is common line to the two triangles which is represented through 1, 2, 4 and 2, 3, 4. A line is drawn joining I₁₂ & I₁₄. Another line is drawn joining I₂₃ & I₃₄. These two lines shall intersect at point I₂₄.

 Determination of Instantaneous Centres in a Mechanism

Now all of the six instantaneous centres have been find out.

To resolve angular velocity of link 4, I₂₄ is needed that connects link 4 with 2. As angular velocity of link 2 is called as I₂₄ may be considered along links 2 and 4. Letting I₂₄ with link 2, the velocity of I₂₄ shall be equal to ω2 × O₂ I₂₄

or,

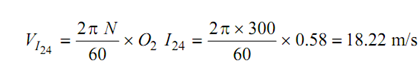
I₂₄ may be considered along link 4 also.

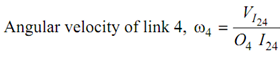
or        

∴ Velocity of point D, V_D = 4.78 m/s.

It's direction is perpendicular to O₄D in the sense of rotation. To find out absolute velocity of C, I₁₃ can be utilized

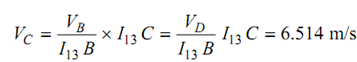
The direction of V_C is perpendicular to the line I₁₃C.