Drawing Karnaugh Maps:

Karnaugh map also called as K-map is the visual representation of SOP solution. To depicted this, let us consider the following example.

                         Y = F (A, B) = ∑ m (1, 2, 3) = A¯ B + A B¯ + A¯ B¯

The truth table for this SOP equation is shown in Table

Table: Truth Table

Following are the steps needed to generate the K-map from the truth table:

Start by drawing Figure (a). Write down the value of suffix of minterms or the equivalent decimal numbers as illustrated in Figure (b).

From the truth table of Table, write down the values of Y for the corresponding minterms. The values of Y for the minterms which are there is the SOP equation is 1, for other minterms it is 0.

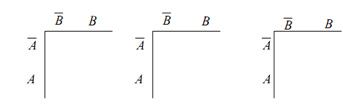
(a)                                      (b)                                                (c)

Figure: Steps for Construction of 2-variable K-map

Likewise, we can construct 3-variable K-maps for any SOP equation involving 3 Boolean variables. For instance, let us consider the following SOP equation :

Y = F (A, B, C) = ∑ m (3, 4, 5)

whose truth table is illustrated in Table

Table: Truth Table

Following the same three step process, we may construct the K-map from the truth table as illustrated in Figure

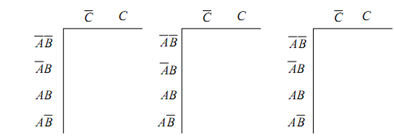
(a)                                                    (b)                           (c)

Figure: Steps for Construction of 3-variable K-map

At last, we may also construct the 4-variable K-map by using the same procedure as depicted in Figure

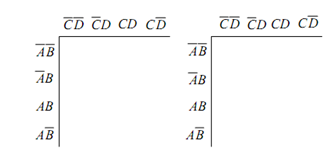
          (a)                                           (b)

Figure: Construction of 4-variable K-maps