Kaldor-Hicks criteria in a production economy:

The Kaldor-Hicks criteria in a production economy can be explained through the  GUPF  and the  various allocation possibilities within them.  Thus,  an allocation  is  superior to another if it  is possible that the winners compensate the losers for moving to the former (Kaldor) or if the losers bribe the winners not to move to the former (Hicks). In a production context, there are now two
forms of  the Kaldor criteria:

- The strong Kaldor criteria requires any compensations to be  a  lump-sum transfer  between  individuals  and thus,  by  not  allowing production  to change as part  of the compensation, one  is confined to making  transfers within a given UPF;

- The  weak Kaldor criterion allows  production  to change  as  part  of  the compensation, and thereby the entire GUPF is available.
It  is clear that the weak Kaldor criteria can compare all Pareto-sub-optimal points in the GUPF. However, the strong criteria cannot do so. This is the complication that Kaldor criteria bring  in  a  production economy. This  is explained in the Figure below. As shown in the figure, there are two Utility Possibility Frontiers (UPF's).

Suppose we  want to compare points E  and G. Obviously, E  is Pareto- inferior to F and G is Pareto-inferior  to D, but  it  is not possible to compare E  and G  by  the Pareto criterion. Let us  then employ  the  strong Kaldor compensation test: if we move  from  point E to point G,  it  is obvious that individual B  is  the winner  and  individual A the loser, However,  B  can (hypothetically) compensate A for her  loss and  still remain  better off by offering a compensation that takes the allocation  to point H (note that both G and H are on the same frontier, UPF_F  -  this  is the requirement of the strong Kaldor criteria). At H,  individual A would be at her old utility level, u^A(E),  but  individual B would have utility u^B(H)  > u^B(E). Thus she  is strictly better off and by  the Kaldor compensation criteria allocation G  is superior to allocation E.  

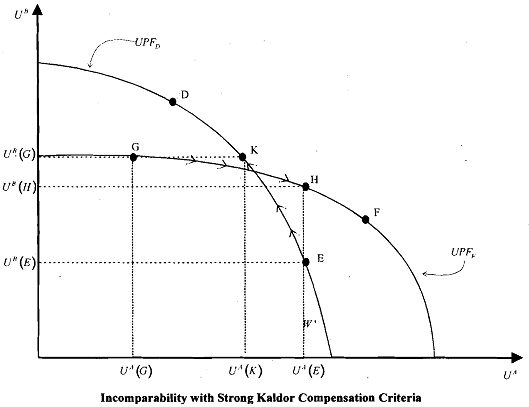
However, suppose we  begin at G and want  to move  towards E. This implies that Individual A is now  the winner and B  the  loser. Yet,  individual A can hypothetically compensate  individual B  by  offering a  transfer  payment  that takes the allocation to point K. At K,  individual B stays at her old utility level u^B(G),  but  individual A  improves her utility position from u^A(G)  to u^B(K).

Thus, by  the strong Kaldor compensation criteria, E is superior to G. And by the same criteria, G  is superior to E. Thus points E and G are not consistently comparable.