Prais-Winsten Procedure:

A problem with the Cochrame-Orcutt transformation (7.20) is the  loss of one observation due  to lagging. The Prais-Winsten method tries to fill this gap. It has been shown by Rao and Griliches (1969), using simulated data (randomly generated data -  also called Monte Carlo experiments) that the best result can be obtained when one  uses  the Durbin estimate  of p discussed  above with  this  procedure.

The basic objective  is  to retain the one lost observation due to lagging. The Prais- Winsten method uses  the following steps:  

1) Multiply the first observation of the regression equation (7.3) by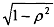

which gives us (7.24). Note that we are multiplying throughout by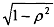

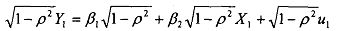
2) Add this transformed  first observation to the Cochrane-Orcutt transformed observations for t==2,3,  ...,  T dnd run  the regression on all T observations  as in (7.20)  above.  It  is easier  if we  define variables 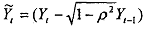and 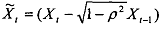for all t = 2,3  ,...,  T. However,  for the first observation we ' define  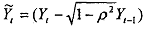= and  similarly for  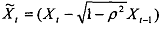Unlike the standard Cochrane-Orcutt method in the second step we can think of this as a regression model without a constant-but with two variables: the first one (earlier constant) now takes the value of  √(1  -  ρ²) for  the  . observation  and  takes the value of √(1-p)  for  the remaining  as therfore. The second variable is the Standard 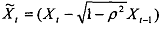for the  first observation  and X_i-ρ_i,  for other observations.