Looking at unit cells

To specify the comprehensive structure of a crystalline solid it is only essential to show one unit cell but interpreting these pictures needs practice. Figure 1 depicts some views of the cesium chloride structure (CsCl, illustrated as MX).

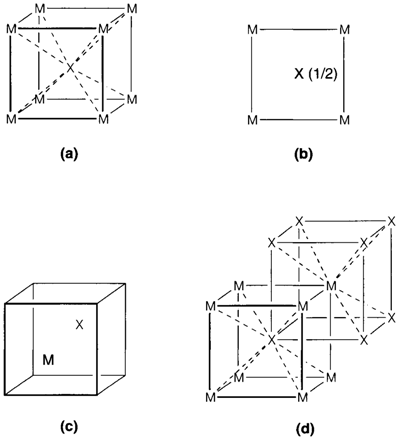
(a) Figure 1a is a perspective view (more precisely termed as a clinographic projection), that is the most general way of showing a unit cell.

(b) Figure 1b depicts a projection down one axis of cell. The position of an atom on the hidden axis is given by specifying a fractional coordinate (example 0.5 for the central atom showing it is halfway up). No coordinate is provided for atoms at the base of the cell.

(c) Figure 1c depicts the atoms shifted relative to the unit cell and emphasizes the fact that what is significant about a unit cell is its size and shape; its origin is arbitrary due to the way where it is repeated to fill space.

(d) In Figure. 1d the drawing has been expanded to depict some repeated positions of the central atom. This facilitates in seeing the coordination of the corner atom.

The most significant feature of any structure is its stoichiometry, the relative numbers of distinct kinds of atoms. The stoichiometry of a unit cell can be determined by counting all the atoms depicted and then taking account of those that are shared with neighboring cells. Whichever atom at a corner of a unit cell is shared among eight cells any at an edge among four, and any on a face between two. So the composition MX in Fig. 1 is arrived at by counting the eight corner M atoms and then dividing by eight to account for sharing. With some experience, this method will seem not necessary. If one simply imagines the unit cell with a shifted origin like in Fig. 1c then it is immediately clear that every cell consists of one M and one X atom.

Other feature characteristic of a structure is the coordination of each atom. There is generally no difficulty in seeing the coordination of an atom in the middle of a unit cell. (For instance, X in Fig. 1a can simply be seen to have eight M neighbours forming the corners of cube. In the projection, Fig. 1b. One requires to remember that the M atoms at the

base of the cell are repeated at the top.) For atoms at corners or edges it is essential to refer what happens in neighboring cells and an extended drawing like Fig. 1d may be helpful: this depicts each M surrounded by eight X neighbours in similar way as the coordination of X.