Displacement:

Let a point P moving in space w. r. t.  fixed rectangular coordinates in space. The position vector of the point P may be denoted through a vector r.

r = x i + y j + z k           . . . (1.1)

On a short interval of time Δ t, the point moves over to the new position P′ explained by the position vector r + Δ r.

r + Δ r = ( x + Δ x) i + ( y +Δ y) j + ( z + Δ z) k  . . . (1.2)

The point is state to have been displaced by Δ r such like that

Δ r = (r + Δ r) - r

= (x + Δ x) i + (y + Δ y) j + (z + Δ z) k - (x i + y j + z k)

or,

Δr = Δxi + Δ y j + Δ z k          . . . (1.3)

 Δr is the displacement of the particle or point within the time interval Δt. this is composed of Δ x along the x-axis, Δ y along the y-axis & Δ z along the z-axis.

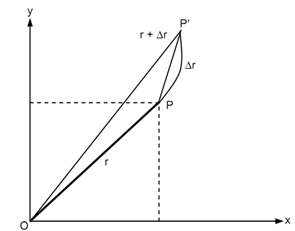
Plane Motion

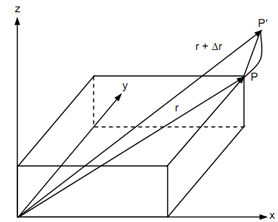
Space Motion