Fuzzy Membership Function

Membership function characterizes the fuzziness in a fuzzy set - here the elements in the set are continuous or discrete- in a graphical form for eventual employ in the mathematical formalism of fuzzy set theory. However the shapes used to explain the fuzziness have only some restrictions indeed. This might be claimed that the rules utilized to describe fuzziness graphically are fuzzy also. Even so, with any formal mathematical structure, some standard terms concerned to the shape of membership functions have been developed over the years, and these terms are defined now, while there are an infinite number of ways to characterize fuzziness, there are an infinite number of methods or ways to graphically depict the membership functions that describe fuzziness. Because the membership function effectively embodies all fuzziness for an exact fuzzy set, its description is the essence of a fuzzy operation or property. Due to the importance of the "shape" of the membership function, a great deal of attention has been focused upon the enhancement of these functions.

The core of membership function for some fuzzy set A is explained as that region of the universe that is characterized by full and complete membership in the set A. That is the core comprises of those elements x of the universe such as μ A (x) = 1.

The support of a membership function for several fuzzy set A is explained as that region of the universe that is characterized by non-zero membership in the set A. That is support comprises of those elements x of the universe such as μ A  ( x) > 0 .

The boundaries of a membership function for several fuzzy set A are explained as that region of the universe having elements which have a nonzero membership but incomplete membership. That is the boundaries comprise of those elements x of the universe such as:

0 < μ A (x) < 1

Such elements of the universe are those with several degree of fuzziness, or merely partial membership in the fuzzy set. Following diagram illustrates typical normal and subnormal fuzzy sets.

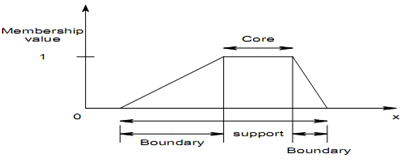
                                                       Diagram of: Core, Support and Boundaries of a Fuzzy Set

There are perhaps more ways to assign membership values of functions to fuzzy variables than there are to allocate probability density function to random variables. This assignment process can be intuitive or it can be based upon some logical operations or algorithmic. Several of the algorithms are as given below:

• Intuition
• Angular fuzzy sets
• Rank ordering
• Inference
• Neural networks
• Soft partitioning
• Inductive reasoning
• Genetic algorithms
• Fuzzy statistics
• Meta rules

Last two methods listed are not addressed in this section due to the wealth of information available in other texts and due to the relative complexity and depth essential to address them adequately.