Application Of Fuzzy Logic In Flexible Manufacturing System Or Fms

Generally, while a Flexible Manufacturing System or FMS is being planned, the objective is to design a system that will be efficient in the production of the entire range of parts. It cannot be achieved till the design, production controlling, scheduling, and planning stages work well. A Fuzzy Based Scheduling Model for FMS which is enhanced here aims at making real-time control decisions that involve dynamic scheduling and variable part routing utilized to solve scheduling problems in FMS environments.

Fuzzy logic, though a mathematical technique, defines its behavioral framework throughout a compact linguistic rule base.  This has the capability to simultaneously consider multiple criteria and to model human experience in the form of easy rules. Moreover, the advantage of the fuzzy logic system approach is that this is incorporates both numerical and linguistic variables. The fuzzy based scheduling, in this sectioned, is designed to resolve the problem of selecting the best part routing for a specified job which is the sub-problem of scheduling in a flexible manufacturing cell or FMC.  In particular, we will demonstrate how to obtain scheduling through a proposed fuzzy model as demonstrated in following Figure.

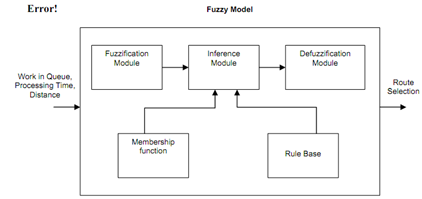
                                                         Figure:Fuzzy Model for Route Selection

The arrangement of the FMC hardware is shown in following diagram. There are p various part types, here each part type requires four operations. All operation can be done by any of the machines with various processing time. A Job consists of the work to be completed for the current scheduling horizon. A job has n parts to be processed on four machines, here parts can follow various routings among four machines. Each machine is capable of performing various operations; however no machine can process more than one part at a time. All part type has several option routings. Operations are not divided or interrupted while started. Set up times are independent of the job sequence and can be involved in processing times. The scheduling problem is to decide which option routes should be selected for all part type.

The procedures of modeling the fuzzy based scheduling are as given below:

The route selection depends upon three fuzzy time factors; the number of parts already waiting in all machine buffer in terms of sum of processing time, how long this will take to done the requested operation and the traveling part time via the route. Thus, for our problem the selected fuzzy variables are termed as Work in Queue, Distance and Processing time, whose base variables are t_ijk, t_i, and t_ij, respectively. They are the input variables utilized for the Route selection reason which is chosen as the output variable.

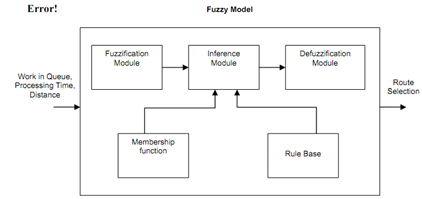
                                                 Figure: Configuration of Flexible Manufacturing Cell

The fuzzy sets of all universe of discourse are labeled as the term set appears in Table 5. The fuzzy sets of work in queue are indexed like SW, MW, and LW, indicating long, medium and short work in queue. The fuzzy sets of processing time are indexed like SP, MP, and LP, representing long, medium and short processing time. The fuzzy sets of distance are indexed also as ST, MT, and LT, indicating long, medium and short travel time. The universe of discourse for these variables is [0, max], and each universe of discourse is explained via three fuzzy sets. The membership functions for all fuzzy set are triangular except at extreme left and right as demonstrated in following diagram (a), (b), and (c), respectively.

                                                Table no.5 of: Definition of Fuzzy Variable

Intuitively, we have to define another linguistic variable representing the route selection. Suppose denote it by Route selection and its base variable by Rs. Suppose those Rs [0, 10] and those we wish the fuzzy model to deal along with the nine distinctions characterizing the route selection. Further, the universe of discourse of Rs has nine fuzzy sets. The membership functions for all fuzzy set are triangular. These fuzzy sets are labeled like the term sets displayed in Table 5. This sets of term are MN, NL, LO, NA, AV, PA, HI, PH and MX, which stand for minimum,  low, negative low, negative average, positive average, average, high, positive high, and maximum, correspondingly.