Force On Shaft and Bearing Due To Single Revolving Mass:

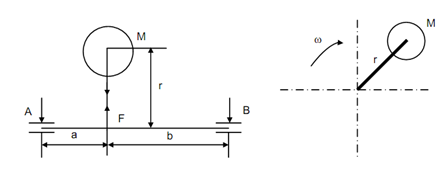
Given fig 1 shows a revolving mass associated to a horizontal shaft that is supported by two bearings. The mass M is at any radius r from the axis of the shaft. The mass is associated to the shaft at distance a from bearing on the left and at distance b from right hand bearing so that the span of the shaft among the bearing is a + b, that means distance among bearings A and B. The eccentricity is because of the tolerances assigned, the restricted accuracy of the manufacturing machines and non-homogenity of the material.

The shaft is rotating along an angular velocity ω rad/s. A dynamic force F shall pull the shaft towards the connected mass M.

F = M ω² r

The force F shall be a bending force on the shaft and shall cause bending moment. Extra bending stress shall be induced and reactions at bearings A and B will take place. The reactions RA and RB may be calculated by considering the equilibrium. They are following

R_A  = (b/ a + b) M ω² r

R_B   = (a/ a + b) M ω² r

These reactions on bearing shall rotate with the mass, therefore will cause fatigue damage. The wear of bearing all over the circumference shall increase. The shaft shall be subjected to bending moment whose maximum value will take place at the section where the mass M is linked to the shaft. The bending moment under the revolving mass shall be following

 BM = (ab /a + b) M ω² r

 While the reactions at the supports become more than the tolerable limits of bearings, the balancing is done.