Estimate reactions at bearings:

A shaft of circular cross-section of diameter 50 mm is supported in two bearings at a distance of 1 m. A mass having 20 kg is attached to the shaft such that its centre of gravity is equal to 5 mm from the axis. The mass is located at a distance of 400 mm from left hand bearing. To ignore unequal wearing of bearings, the designer places the mass in the centre of the span. Estimate reactions at bearings, maximum bending moments (BM) and bending stresses if the shaft rotates at 750 rpm.

Solution

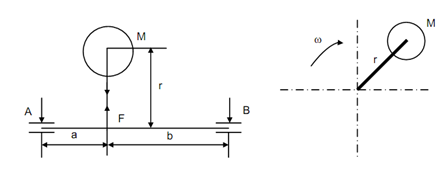
The force caused on shaft due to rotation = F

ω= 2π N /60 = (2π× 750)/60 = 78.54 rad/s

ω= (ω / g )ω² r

Use M= 20 kg, ω = 78.54 rad/s, r = 5 × 10^{- 3} m

F = 20 × (78.5)² × 5 × 10^{- 3} = 616.85 N

(a)    Case I

Mass at a = 400 mm from left hand (LH) bearing

b = 1000 - 400 = 600 mm

a + b = 1000 mm

A - left, B - right hand bearing

∴             R_A  =  (b/a + b) F =

                                = (600/1000)× 616.85

 Or   R_A  = 370.1 N

 (b)

 and R_B  = F - R_A  = 616.85 - 370.1

 (c)

 And R_B  = 246.74 N

∴ Maximum BM = R_A. a = 370.1 × 400

or            BM  = 148.04 × 10³  Nmm

Bending stress is given by following

σ  = 32 BM/ π d³

where d = 50 mm = shaft die

σ _b  = (32 × 148.04 / π× (50)³) × 10³     

or σ_b  = 12.06 N/mm2

Case II

 Mass at the centre of span, that means a = b = 500 mm

∴             R _A   = R _B = F/2 = 616.85/2 = 308.425 N

∴ Maximum BM, (F/2) × a = 308.425 × 500 = 154.213 × 10³ Nmm

∴ σ_b =32 BM/ π d³

= ((32 × 154.213)/ π× (50)³⁾ × 10³

σ_b = 17.35 N/mm²