Determine the mass:
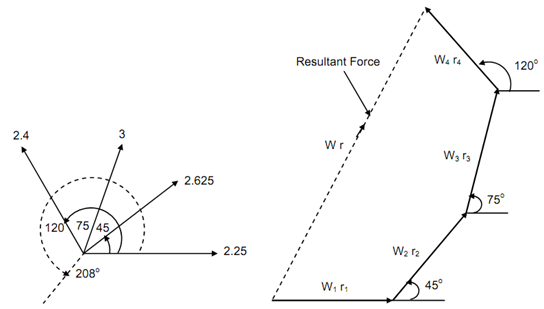
Four masses W1, W2, W3 and W4 at radii of 225 mm, 175 mm, 250 mm and 300 mm are associated at angles of zero, 45o, 75o and 120o through horizontal line as illustrated. If the shaft rotates at 500 rpm, determines what unbalanced force acts upon the shaft and at what angle from mass W1. If a mass to balance the system may be placed at a radius of 200 mm, determine the mass.
Take W1 = 1000 N, W2 = 1500 N, W3 = 1200 N and W4 = 800 N
Solution
W1 r1 = 2.25 × 105
W2 r2 = 2.625 × 105
W3 r3 = 3 × 105
W4 r4 = 2.4 × 105
Figure 5 illustrated the orientation of disturbing forces along magnitudes (proportional to W r). Force polygon is illustrated in Figure 5(b). From the polygon the unbalanced W r = 7.75 is at an angle of 207.5o.
(i) (ii)
The unbalanced force = (W/g) ω2 r
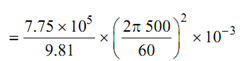
= 2.166 × 105 N
If radius at which balancing mass is located is 200 mm.
Then
W r = 7.75 × 105
W = (7.75 × 105 )/200
W = 3875 N
M = W/ g = 3875/9.81
= 395 kg
Another method is to resolve W r along vertical and horizontal direction and determine their resultant.
W r (H ) = 2.25 + 2.625 cos 45 + 3 cos 75 + 2.4 cos 120
= 2.25 + 1.856 + 0.7765 - 1.2
= 3.6765
W r (V ) = 2.625 sin 45 + 3 sin 75 + 2.4 sin 120
= 1.856 + 2.9 + 2.0785
= 6.83
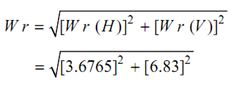
= 7.76
θ= tan-1 ( W r (V )/ W r (H ))
= tan -1 (6.83/3.675)
= tan-1 1.8583 = 61.7o
Note down that W r is the resultant unbalance force that will act upward. The balancing mass shall be placed opposite to it that means downward as illustrated in broken line in Figure 5(a). 207.5o is the measured angle. The calculated value of the angle is equal to 61.7 + 180 = 241.7o.
Compare the Values
From polygon construction
W r = 7.75, θ = 241.4o from W1
From calculation
W r = 7.76, θ = 241.7o for W1.