Risk measurement models:

Generally, a measure is an operation for assigning a number to something. A metric is our interpretation of the assigned number. When we apply a measure, the number obtained is a measurement.

There are many metrics of risk-volatility, duration, etc. We call these risk metrics. A measure that supports a risk metric is called a risk measure. The value obtained from applying a risk measure is a risk measurement. 

We have already learnt that prices of bonds with longer maturity are more sensitive to interest rate changes than bonds with shorter maturity period. But this is only a rule of thumb. Maturity by itself is not a complete indicator of interest rate sensitivity. A different measure of time-length called duration does give a direct measure of interest rate sensitivity. We discuss duration as a measure of interest rate sensitivity in this section.

Duration is a term used in the analysis of fixed-income instruments. At its most basic level, duration is a measurement of how long in years it takes for the price of a bond to be repaid by its internal cash flows. It is an important measure for investors to consider, as bonds with higher durations (given equal credit, inflation and reinvestment risk) may have greater price volatility than bonds with lower durations. It is an important tool in structuring and managing a fixed-income portfolio based on selected investment objectives. The price of a bond or any fixed-income investment is determined by summing the cash flows discounted by a rate of return. The rate of return can change at any time period and will be reflected in the calculation of an investment's market price. The sensitivity of a bond's value to changing interest rates depends on both the length of time to maturity and on the pattern of cash flows provided by the bond. There are many variables associated with pricing a bond. Changes in each of these variables, taken separately and in combination, can have a significant effect on price. Duration is a calculation that brings all these factors together in one number, allowing a measurement of a bond's price sensitivity to changes in maturity and interest rates. The common objective behind the different definitions of duration is to measure the price sensitivity or market risk of a fixed-income security to changes in its yield. Bonds of similar duration will have similar price movements for a given movement in interest rates.
In general terms, we may say that duration of a fixed-income security like a bond is the weighted average of the times that  payments, that is, cash flows, are made. The weights are the present values of the individual cash flows. Duration is the weighted
average maturity of its cash flow stream, where the weights are proportional to the present value of cash flows. Formally, it is defined as:

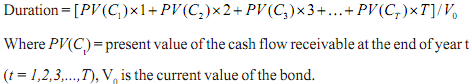
Let V be the price of the bond, and y the yield, then the proportional change in the price of a bond in response to the change in its yield is as follows

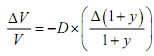
where ΔV/V is proportional change in price, D is duration, and y is yield.