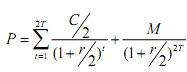Market risk:

We focus in this unit on debt instruments and hence on the interest rates associated with these.  We largely concentrate on debt instruments about which we make the assumption that these are free of risk of default by the issuer. We also assume away complications arising from taxation. For the moment we assume also that there are no embedded option features associated with the bond. Before proceeding further towards the pricing of the bonds let us familiarise ourselves with some basic concepts.

The term to maturity or maturity of the debt contract is the number of years during which the issuer (borrower) has promised to meet the conditions of the debt instrument. The amount that will be repaid by the borrower is called the principal. A bond is a special type of debt contract, and the amount paid at maturity is called the par value, maturity value or face value. If the price at which a bond is sold is exactly the same as its nominal value, we say the bond is sold at par. If the price is higher than the nominal value, we say the bond is sold above par, and if it is sold below the nominal value then we say it is sold below par. The financial contract between the issuer of the bonds and the purchaser of the bond is called the bond indenture.

A debt contract's coupon is the periodic interest payment that is paid to the holders of the debt instrument. The name comes from the fact that in olden there would actually be coupons handed out to show the payments. The coupon rate, multiplied by the unpaid outstanding principal gives us the rupee amount of the coupon payment.

There are certain debt instruments for which no periodic coupon interest is paid over the life of contract. Instead, the principal along with the interest is paid at the maturity date.  Such debt instruments are called zero-coupon instruments. Now a discussion of bond valuation is in order. The value of a bond is equal to the present value of the cash flows expected from it. For simplicity, let  us assume that the coupon interest rate stays constant for the term of the bond. Let us also assume that coupon payments are paid only once a year, every year on an annual basis for the life of the bond and that the bond will be redeemed at par on maturity. In this case, the value of the bond of the bond is given by: 

There are bonds that pay interest semi-annually, that is, twice a year. In this case, the unit period is six months, rather than a year. In this case, interest payment becomes C/2. The total time period becomes 2T, and in this case 2T shows the number of half-yearly periods, and the discount rate becomes r/2 to get the discount rate applicable to half-yearly periods. With these modifications, the basic bond valuation becomes