Modelling insurance market with adverse selection:
We will discuss the important features of Rothschild-Stiglitz theorem, which basically highlights the following result:
When information is private, giving rise to the problem of adverse selection, market outcomes cannot produce Pareto efficiency. Particularly, when there is imperfection in the market such that one of the parties to a transaction is better informed than the other, inefficiencies would crop up. You will notice equilibrium of such a market that violates the first welfare theorem.
Let us see how the model works. For this purpose, we will follow the presentation as well as notations of Autor, 2004. Suppose a risk-averse individual faces two states of the world in which her initial wealth is characterised by no-accident and accident. If there is no accident, wealth is w and with accident, wealth is w - d (where d > 0 stands indicates damage).

where the vector a = (a1, a2) describes the insurance contract. You can think that the insurance premium a,, is paid in both the accident and no-accident states. Hence, a, is the net payout of the policy in event of accident. If you denote the probability of an accident as p, then an individual purchases insurance when the expected utility of being insured exceeds the expected utility of being uninsured, i.e.
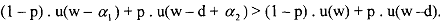
On the other hand, the insurance company will sell a policy if expected profits are non-negative, i.e.,
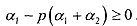
Let us assume a competitive market, so that this equation holds with equality. Therefore, in equilibrium:
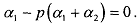
To derive the equilibrium conditions of the model, we follow the formulation Rothschild-Stiglitz who propose the following conditions:
1) No insurance contract makes negative profits (break-even condition).
2) No contract outside of the set offered exists that, if offered, would make a non-negative profit. For, if there were a potential contract that could be offered and would be more' profitable than the contracts offered in equilibrium, then the current contracts cannot be an equilibrium.