Permanent Adjustments

The three critical axes of a dumpy level are line of collimation and bubble tube axis and instruments vertical axis as display in Figure 5. These are correlated in subsequent way with each other.

(a)  Line of collimation and bubble tube axis are parallel to each other.

(b)  The bubble tube axis is normal to vertical axis of the instrument.

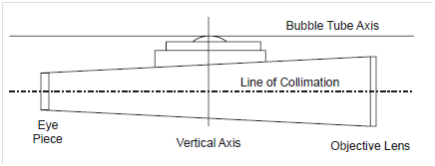
                                                   Figure : Critical Axes of Dumpy Level

These conditions are ensured by the manufacturer during production of instrument. Therefore, because of continuous usage some wear and tear do occur and the above relationships among critical axes are disturbed. This will introduce instrumental error in level measurements. For accuracy, the level is required to be adjusted so as to satisfy the above conditions. Because these adjustments are needed only while the instrument's internal setting is disturbed during usage and not needed every time the instrument is setup, these are termed permanent adjustments.

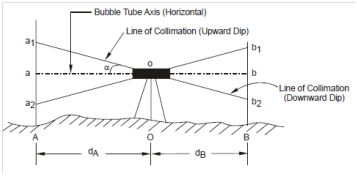
                                                        Figure : Level out of Adjustment

When the instrument is not adjusted, the line of collimation will not be parallel to the bubble tube axis (horizontal) but inclined either upwards or downwards (Figure 6). Let this inclination be α. An error is introduced in recording the levels. Let us determine the true difference in levels of station A and B situated at a distance of d_A and d_B associatively from instrument setup at O. Then line a₂ob₂ represents the true line of collimation (horizontal). Therefore, since the adjustments are out of order, the actual line of collimation will be a₁ob₁ along with downward dip and a₂ob₂ within upward dip of line of collimation.

If          Aa₁ = observed reading of staff at station A Then error in reading at A will be Aa₁ - Aa = d_A tan α

Similarly, when staff is held at station B,

Bb₁ = Observed reading; Bb = actual reading

Error in reading at B is Bb₁ - Bb = d_B tan α. True difference in levels of stations A and B will be

Bb - Aa = {Bb₁ - d_B tan α} - {Aa₁ - d_A tan α}

= {Bb₁ - Aa₁} - {d_B tan α - d_A tan α}           . . . (4.1a)

Eq. (4.1a) will indicate the error in adjustment and also indicate that it is proportional to distance of staff station from instrument station. One way to eliminate this error would be to remain the instrument station O at exactly equidistant from staff stations A and B, i.e. d_A = d_B. It will change Eq. (4.1a) as

[Bb - Aa] = True level difference at A and B

= [Bb₁ - Aa₁]