Kennedy's Theorem:

This theorem is also known as 'Three Centres in Line Theorem' or 'Aronhold-Kennedy Theorem of Three Centres.' This theorem said:

'If three bodies are in relative motion w . r. t.  one another, the three instantaneous centres of velocity are collinear.'

 Proof

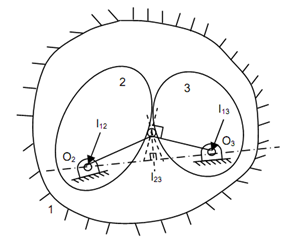
Given fig shows three links 1, 2 and 3 in relative motion w. r. t. one another. Link 1 is fixed while links 2 & 3 contain motion. The instantaneous centres I₁₂ & I₁₃ are at hinges O₂ and O₃ respectively. Regarding these points, links 2 & 3 rotate. The third instantaneous centre I₂₃ also lies in the plane of motion. If I₂₃ does not lie on the line joining I₁₂ & I₁₃, it can lie above or below this line.

Consider its position above the line joining I₁₂ & I₁₃ as illustrated in the figure. Instantaneous centre I₂₃ may be considered with link 2 & link 3. Referring I₂₃ as a point along link 2, its velocity ought to be perpendicular to line joining I₁₂ & I₂₃. If I₂₃ be referred along link 3, its velocity ought to be perpendicular to the line joining I₁₃ and I₂₃ these two directions are different. However by definition I₂₃ ought to have similar velocity whether it is referred to be with link 2 or 3 and in this case this is not so. It means I₂₃ may not lie above the line joining I₁₂ & I₁₃. Alike case shall occur if point I₂₃ is considered below the line I₁₂, I₂₃. Thus, I₂₃ may lie on the line I₁₂ I₁₃ just or else the directions of velocity shall be different while it is considered with link 2 & 3. it proves that the three instantaneous centres I₁₂, I₁₃ and I₂₃ are collinear.

    Kennedy's Theorem