Instantaneous Centre of Rotation:

While a mechanism executes plane motion, a link associating to the planar mechanism corresponds to one of the three following cases as:

(a) Linear motion, like that of a piston in an internal combustion engine,

(b) Rotary motion, like that of a crank rotating regarding a fixed axis, and

(c) Plane motion, as that of connecting rod of an engine.

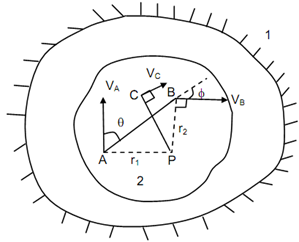
At a particular instant, a link executing general plane motion may be thought of as rotating regarding an imaginary centre. In given figure a rigid body 2 executes plane motion w. r. t. fixed body 1. Assume there is any two obituary points A & B on body 2. The velocities of points A and B are illustrated in the Figure by V_A and V_B respectively. The perpendiculars to the directions of velocities V_A and V_B have been drawn at A & B. These perpendiculars meet at point P. Assume AP & BP is r₁ and r₂ respectively.

The velocity of point A along AB = V_A cos θ

The velocity of point B along AB = V_B cos φ

Instantaneous Centre of Rotation

As body 2 is rigid, thus, distance AB does not alter. Only this is possible while velocity of B relative to A, that is component along AB, V_BA is zero.

 Since

         V_BA  = V_B  cos φ- V_A cos θ

 Or    V_B  cos φ - V_A  cos θ = 0

Or     V_B  cos φ = V_A  cos θ

                      . . . (4.1)

From triangle ABP, we have following

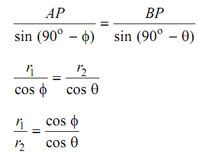...........(4.2)

From Equations. (4.1) & (4.2) 

            . . (4.2)

Thus, the velocities of points A & B are proportional to distance from P and have directions perpendicular to the lines joining respective points to P. therefore, momentarily, the rigid body 2 may be thought of as being in pure rotation around the point P. This point P is known the instantaneous centre of velocity and, in this; its instantaneous velocity is zero. The velocities V_A and V_B of points A & B are absolute velocities. The instantaneous centre P has been finding out by using these velocities. This instantaneous centre of moving body 2 is in relation to fixed body 1 and so, it has velocity equivalent to zero. So, on the other hand, the instantaneous centre of velocity of body 2 in relation to fixed body 1 may be defined like a point which contains no velocity. This point P may be used to resolve absolute velocity of a point in body 2. The velocity of any point C at this point is given by V_C  = PC × V _B/ r₂ and the direction of the V_C is perpendicular to the line  PC. Like the orientation of body 2 alters, the position of instantaneous centre P also modified.