RINGS AND CLUSTERS

Introduction

Ring and cluster compounds arise in several areas of chemistry.  Rings are most frequently formed by nonmetallic elements with directional covalent bonding.  They include homoelement  rings like S₈ (1) and benzene C₆H₆ and ones with heteroelement bonding like S₂N₂ (2), borazine B₃N₃H₆ and the silicate ion [Si₃O₉]^3-. Clusters are polyhedral arrangements of atoms found very broadly in the periodic table: nonmetals (example P₄  3 and boranes discussed below),  main-group metals (example [Pb₅]^2- 4) and transition  metals (frequently  with  ligands like CO; see Topic H9). Heteroelement bonding is also possible like in the A₄B₄ structure 5, adopted by the As₄S₄ (where A=As and B=S) and S₄N₄ (where A=S and B=N).

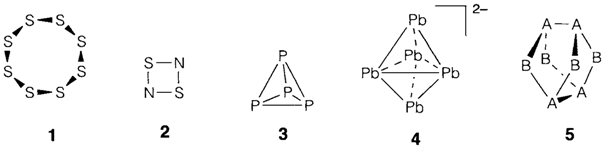
Complex molecular structures do not essentially need complex bonding models, and certainly much of organic chemistry can be understood using rather elementary ideas. Some inorganic ring and the cluster compounds like P₄ and S₈ can be understood in terms of elementary electron pair bonds; the octets are accomplished in each case with two nonbonding electron pairs for each S atom and one for each P. Likewise in As₄S₄, each such as forms three bonds and one lone-pair, each one S atom two bonds and two lone-pairs. The oppposite arrangement of S₄N₄  is little much harder to understand but may still be accommodated  in  simple ideas by placing a formal negative charge on each two-bonded N and a formal  positive charge on each three-bonded S; as supposed for bonds among  formal  S⁺ entities,  the S-S bonds (A-A  in 5) are not normally long and weak.

Several rings and clusters, though, cannot be understood within the two-center two-electron bond framework.  This is sometimes expanded  by assuming resonance,  for instance  between  the two Kekulé-type structures for benzene (6). A more natural technique is to extend the molecular orbital (MO) technique to many atoms. The so-called Hückel theory of the ring systems makes significant  predictions relevant to inorganic molecules like S₂N₂. Clusters like boranes also require a delocalized  MO approach. Wade's rules provide a helpful systematization of the principles involved and can be expanded to other systems.