ELEMENT STRUCTURES

Sphere packing

Element structures in which chemical bonding is nondirectional are best introduced by considering the packing of equivalent spheres. Close-packed structures are ones that fill space most efficiently. In two dimensions this is accomplished in a layer with each sphere surrounded hexagonally by six others. 3-d structures are developed by stacking

these layers so that the spheres in one layer fall over the hollows in the one below, as displayed in Fig. 1a. Having placed two layers, labeled A and B, there are different positions for the spheres in the third layer. They can be placed directly over spheres in the first layer A to give a sequence denoted as ABA. Furthermore, the spheres in the third layer can be placed in positions where there are gaps in layer A; two such type of spheres labeled C are displayed in Fig. 1a. A regular packing based on this latter arrangement would then place the fourth layer directly over layer A, giving a sequence denoted as ABCA. The simple most 3-d close-packed structures are based on these two regular sequences of layer positions:

ABABABAB...gives hexagonal close packing (hcp);

ABCABCABC...gives cubic close packing (ccp).

These structures are demonstrates in Fig. 1b and c. correspondingly. In the ccp arrangement, the successive close-packed layers are placed along the body diagonal of a cube. The unit cell displayed is based on a cube with atoms in the face positions and the structure is also known generally as face-centered cubic (fcc).

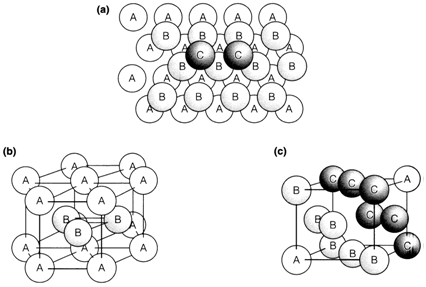
Fig. 1. Close-packed structures, (a) Stacking of layers showing the sequence ABC (see text); (b) the hcp structure; (c) one unit cell of the fcc structure.

In both hcp and fcc structures each sphere is surrounded by 12 others at similar near-neighbor distance. (There are six in similar close-packed layer and three each in the layers below and above) both structures give 74% filling of space by the spheres, with the remaining 26% outside them, if the spheres are in contact. This is the optimum space filling possible with equal spheres. Likewise close-packed structures can be constructed from more complicated sequences of layers like ABABCABABC..., or even with random sequences. Even though these are sometimes found, mainly close-packed structures are of the simple hcp or fcc types.

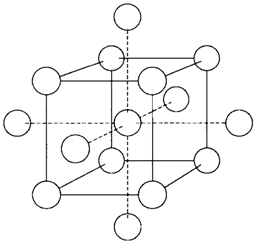
Other structure that gives quite efficient space filling (68% compared with 74% above) is the body-centered cubic (bcc) one demonstrated in Fig. 2. Every atom has eight near-neighbors, but there are six others (also displayed in the figure) little further away.